Reply to 'Mathematical Inconsistency in Solomonoff Induction?'
Date: 2020-09-04This is a reply to this LessWrong post.
I went through the maths in OP and it seems to check out. I think the core
inconsistency is that SI implies 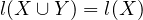 . I’m going to redo the maths
below (breaking it down step-by-step more). curi has
. I’m going to redo the maths
below (breaking it down step-by-step more). curi has 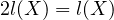 which is the
same inconsistency given his substitution. I’m not sure we can make that substitution
but I also don’t think we need to.
which is the
same inconsistency given his substitution. I’m not sure we can make that substitution
but I also don’t think we need to.
Let X and Y be independent hypotheses for Solomonoff induction.
According to the prior, the non-normalized probability of X (and similarly for Y ) is:
what is the probability of 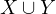 ?
?
However, by Equation (1) we have:
thus
This must hold for any and all X and Y .
curi considers the case where X and Y are the same length, starting with Equation (4)
but
and
so
curi has slightly different logic and argues 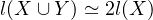 which I think is
reasonable. His argument means we get
which I think is
reasonable. His argument means we get 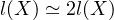 . I don’t think those steps are
necessary but they are worth mentioning as a difference. I think Equation (8) is
enough.
. I don’t think those steps are
necessary but they are worth mentioning as a difference. I think Equation (8) is
enough.
I was curious about what happens when 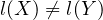 . Let’s assume the
following:
. Let’s assume the
following:
so, from Equation (2)
by Equation (3) and Equation (10)
but Equation (9) says 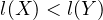 – this contradicts Equation (11).
– this contradicts Equation (11).

So there’s an inconsistency regardless of whether 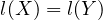 or not.
or not.
You can leave a comment anonymously. No sign up or login is required. Use a junk email if not your own; email is only for notifications—though, FYI, I will be able to see it.
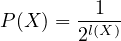
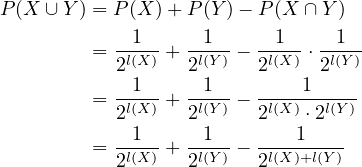
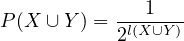
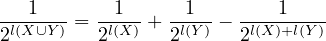
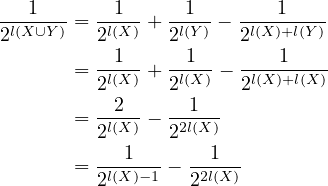
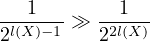
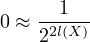
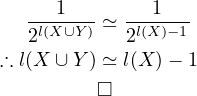
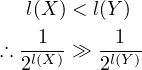
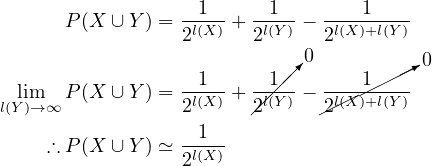
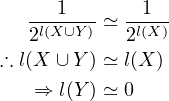
Comments powered by Talkyard.